
For a physicist, inspiration for better designs and techniques can strike at any time. For a hungry physicist, inspiration can strike at mealtimes, specifically. Case in point: a cooking method that comes easily to a seasoned chef, but provides frustrations for at-home cooks — making a crêpe. Two researchers, in their search for the perfect crêpe, used simulation to see if they could cook this classic cuisine more evenly…
Crêpe-Making 101 and the Optimal Coverage Problem
Crêpes are both versatile and delicious. The thin French pancake is the perfect vehicle to fill with foods both sweet and savory — like smoked salmon or strawberries and cream. The basic ingredients are staples that you probably already have in your kitchen: flour, eggs, milk, sugar, butter, and salt. The ingredients seem simple enough, but crêpes are deceptively difficult to make. It is a delicate dish that needs to be light; thin; fluffy; and above all, flat, with minimal lumps so it can cook all the way through. But this is easier said than done, as many of us can attest!
So, what is the best way to make crêpes? To get the optimal thinness and shape for a crêpe, you’re going to need specialized equipment (no simulation software…yet) including:
- Whisk, mixer, or blender
- Refrigerator
- Spreader
- Spatula (if desired, for flipping)
- Nonstick frying pan
For the batter, you whisk or blend the ingredients until the consistency is thin; almost runny; and, of course, lump-free. For sweet crêpes, add some extra sugar or a dash of vanilla; for savory, add some herbs. Then, it is very important to let the batter rest, either on the counter for 30 minutes or, even better, chilled in the fridge overnight. This will ensure that the crêpe batter has time to get rid of all the bubbles generated from the mixing process. Once rested, the batter can be ladled out into the heated pan. How the batter spreads in the pan matters, as two fluid dynamicists who decided to get to the bottom of an optimal coverage problem (and the pan) found out.
Optimal coverage for crêpes means that the end result is uniformly thin, hole free, and perfectly circular. But because the batter starts to cook immediately upon hitting the pan and as it spreads, this uniform coverage is harder to achieve than it seems! Many cooks know to tilt the pan and swirl the batter, or use a blade to spread the batter more evenly and get it as flat as possible against the pan surface. While many people know how to perform these techniques intuitively, the physicists behind this project wanted to know if the techniques could be refined, and further, if they could optimize the crêpe-making process as a proof of concept using numerical modeling.

Left: Crêpe batter that was not spread and distributed evenly in the pan. The crêpe doesn’t achieve optimal coverage. Right: The lumpy result.
“The motivation for this study literally comes from the kitchen,” says Edouard Boujo, fluid dynamicist and assistant professor at the École Polytechnique. One Sunday, Mathieu Sellier, professor of mechanical engineering at the University of Canterbury, was making crêpes in his kitchen. He was frustrated by their imperfect shape, and what Sellier called a “persistent niggle” that there ought to be a better way to make them. Finally, his wife had had enough of his complaining. “You’re a fluid dynamicist,” she reminded him. “You should be able to do something about it!”
So challenged, Sellier began his quest to make the perfect crêpe. Joining forces with Boujo, who he met at a conference in Montreal in 2016, the two physicists worked together using the COMSOL Multiphysics® software, bringing their own professional strengths to the table. Sellier is an expert on free-surface and thin films, while Boujo is an expert on optimal control.
Simulating Batter Flow and Hardening on Pan Surfaces with COMSOL Multiphysics®
When it comes to the interaction between substrate kinematics and a liquid layer in fluid dynamics setups, you’re typically relying on centrifugal forces to drive the fluid, and the substrate kinematics to involve a rotation around the vertical axis (with variable angular velocity).
Crêpe making, however, differs in this regard. Instead of centrifugal forces, the batter is driven by gravity, and instead of a single rotation, the pan kinematics involve a transient rotation around multiple axes. Until now, this kind of fluid flow had not been modeled, but the researchers saw it as an opportunity for studies in liquid layer solidification and its application areas.
“What started as a side project soon turned out to be relevant to any situation where a thin liquid film of uniform thickness is desirable,” says Boujo. He explains that this is critical in many industrial processes that need to have a very thin and uniform coating layer, such as those for smartphone displays, solar cells, electronic circuit boards, and more.
Setting up the model required taking equations and strategies from published literature and modifying them for this particular fluid dynamics and optimal control problem. To get the motion of the batter and the pan right, the researchers applied gradient-based optimization, which is often used to solve problems with many optimization variables. This was combined with adjoint sensitivity analysis, which can determine the sensitivity of thousands of optimization variables at a cost similar to the computation of the forward problem.
The researchers chose COMSOL Multiphysics for modeling this optimization problem because they wanted to make sure the numerical scheme would preserve the total mass of fluid, which was easily done thanks to the partial differential equation (PDE) solver in the COMSOL® software. “COMSOL’s flexibility allowed us to implement the adjoint equation quite easily,” says Boujo. Further, LiveLink™ for MATLAB® was a convenient way for them to perform the optimization. “The main code, written in MATLAB®, took care of the descent algorithm, calling on COMSOL® to solve the direct or adjoint equations whenever needed,” says Boujo.
The team also needed to account for the multiphysics nature of the problem in terms of the evolution of the film thickness and the effects of heat transfer and substrate kinematics. First, they modeled the spreading behavior of the fluid on a substrate at rest and on a substrate moving with time-harmonic kinematics; i.e.,
where A_1, A_2, T_1, and T_2 are parameters to be optimized with the Monte Carlo method, such that the film uniformity was improved.
The optimization problem was set up as a minimization problem, because the film uniformity was measured as the squared deviation from a flat profile, {\cal U}(t_f),
where h(x,y,t) is the batter profile, while h_\mathrm{opt} is the profile height when the batter takes the shape of a cylinder.
Then, they dug deeper into the problem by allowing for arbitrary kinematics, \theta(t) and \beta(t), but this increased the number of optimization variables dramatically, which called for the combination of gradient-based optimization and adjoint sensitivity analysis. Furthermore, extreme kinematics were avoided by adding a penalty term, \cal C, to the objective function, {\cal J}_t. The term was scaled with a constant, \gamma, which could be used to allow more or less extreme kinematics,
Evaluating the Results of the Fluid Dynamics Simulation
The results of the study indicate that the gradient-based optimization strategy was superior to the Monte Carlo method. As shown here, when plotting the objective function (left) and the squared deviation from uniformity (right) as a function of the \gamma parameter that prevents extreme kinematics. The left figure shows that the more extreme kinematics allow for flatter crêpes and that the gradient-based optimization (filled circles) is significantly better than the Monte Carlo method. The Monte Carlo method leads to better uniformity when the penalization is large, but the objective function is actually significantly worse (see the left figure). This exemplifies the random nature of the Monte Carlo method rather than any technical superiority.
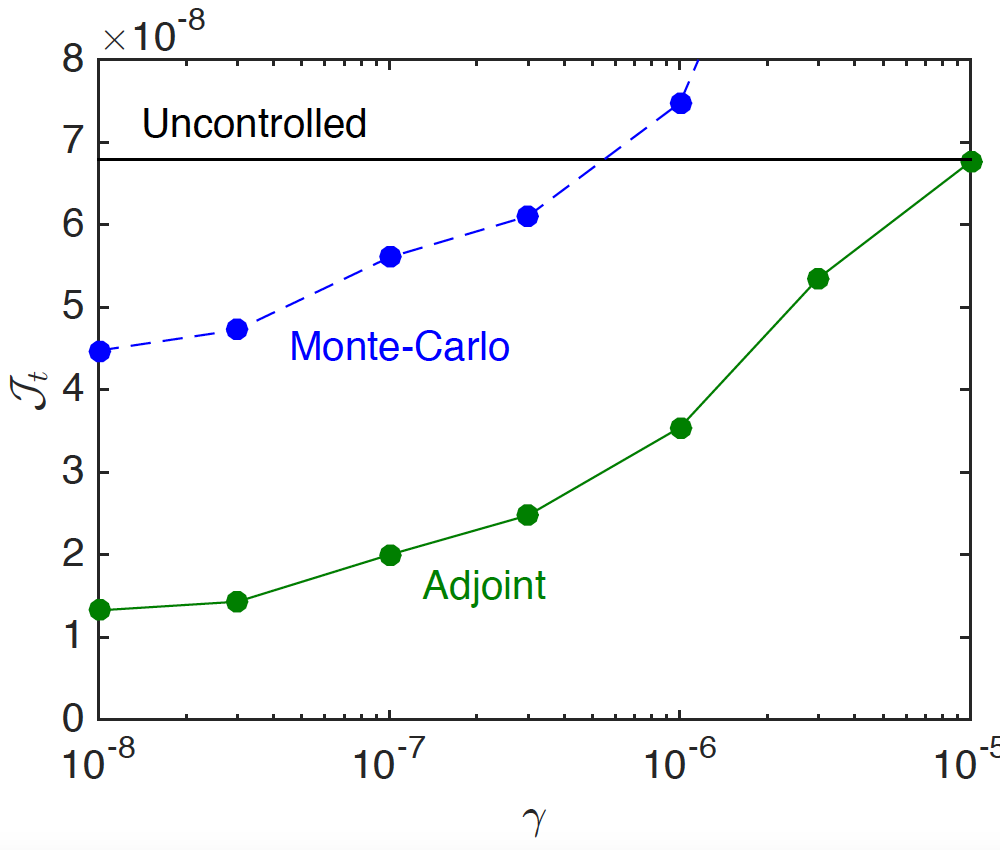
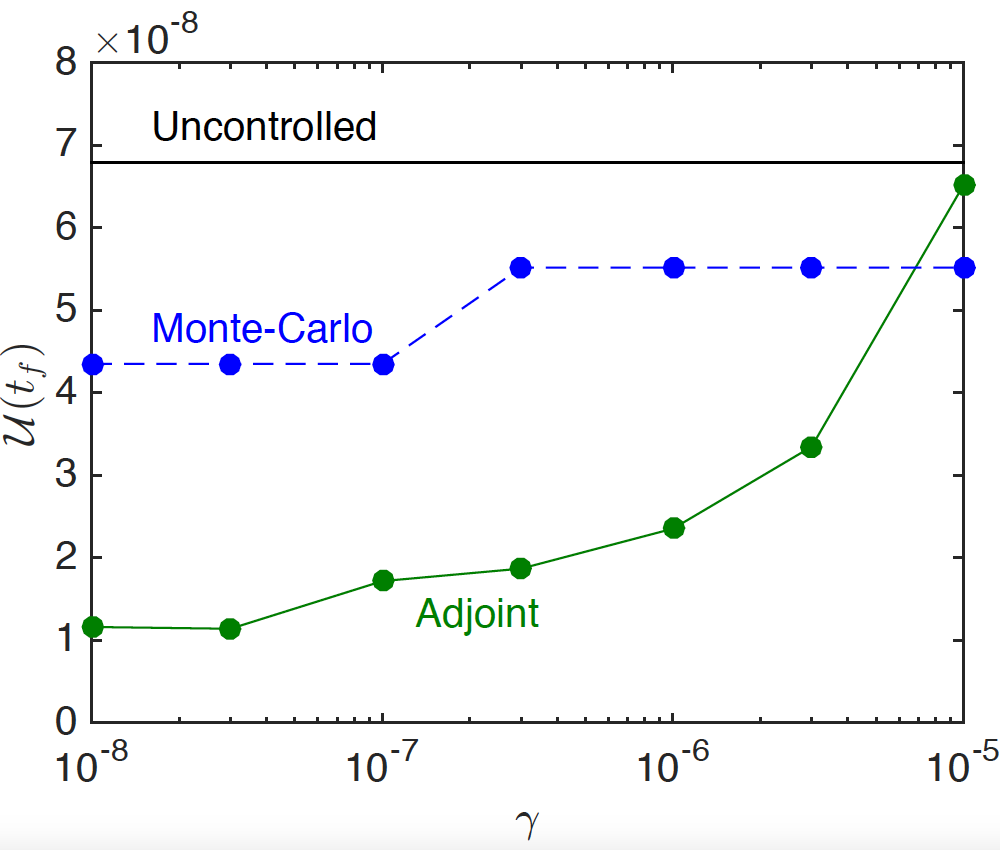
Left: The objective function {\cal J}_t vs. the penalization parameter \gamma. Right: The final uniformity {\cal U}(t_f). Images courtesy Boujo and Sellier.
Further, after finding the best time-harmonic kinematics (below, left), the researchers were able to improve upon these results by finding the best control laws with their adjoint optimization method, thus helping them achieve optimal contours of film thickness (below, right).
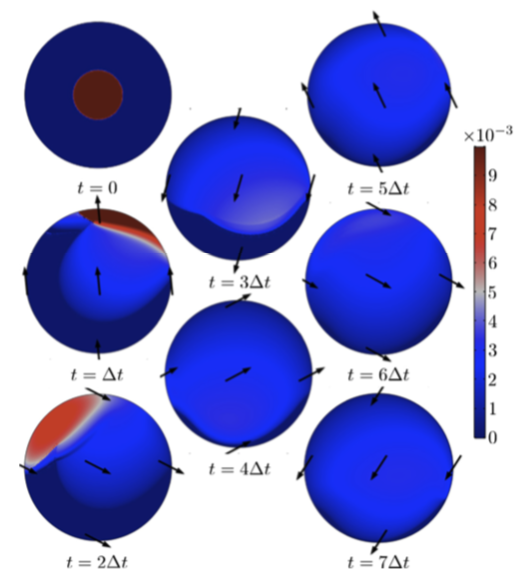
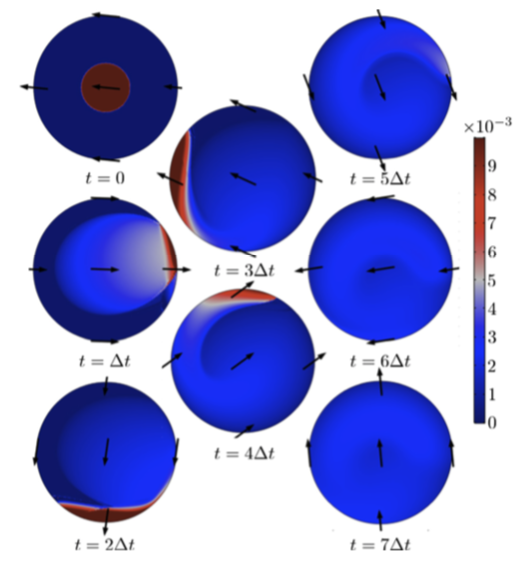
Left: Contours of film thickness h(x,y,t) for the best harmonics kinematics minimizing {\cal U}(t_f), obtained with the Monte Carlo method. Right: Contours of film thickness h(x,y,t) for the best arbitrary control with \gamma = 10^{-8}. The arrows for both results show the direction of the projection of gravity on the surface plane. Images courtesy Boujo and Sellier.
For the final result, you can compare the stationary kinematics with optimal harmonic kinematics and optimal arbitrary kinematics for two values of the penalization parameter \gamma. The final film gets increasingly uniform and smoother for each case. As an added bonus, the gradient-based optimization method is less computationally expensive than the Monte Carlo method.
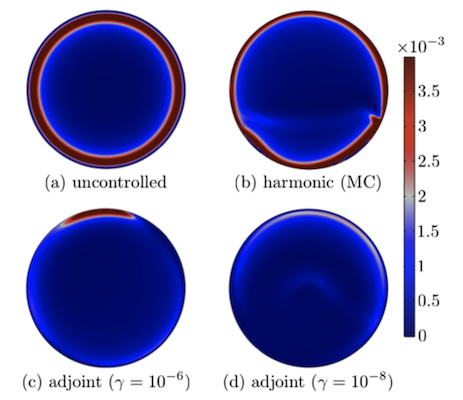
Final thickness gradient squared for the uncontrolled case (a); optimal harmonic control (b); second-best arbitrary control (c); and optimal arbitrary control (d). Images courtesy Boujo and Sellier.
The Best Way to Make Crêpes? It’s All in the Wrist
As for applying Boujo’s and Sellier’s results to make better crêpes? As soon as the batter hits the pan, you should tilt the pan so that all the batter runs to the side. Then, rotate the pan all the way once or twice so that the batter covers the rest of the surface, reducing the steep angle gradually as you go. Put the pan on the stove and in no time, you’ll be saying “voilà — brunch is served!”

While my flipping technique may need some practice (hence the crack), a more even distribution of the batter in the pan (left) yields more even results (right).
Further Food for Thought
Boujo and Sellier realize that the optimal pan motions they got from their findings are quite similar to what cooks already do. “It was great to be able to confirm that people are good ‘intuitive optimizers’, at least in the simple case of crêpe making,” they said.
Further, they soon saw that the benefits of their methods extend beyond the world of cooking. “We are now working on moving toward more complex practical applications,” says Boujo. Through modeling this type of flow, they found that in addition to the thin films required for phone displays and solar cells, in some situations, “moving the substrate may be a good alternative to other techniques currently employed” in industrial processes, like spin coating, blade coating, and vapor deposition.
Whether you’re a home cook who’s been struggling for years to perfect your crêpe-making techniques or an engineer interested in this type of fluid flow, it seems that these two fluid dynamicists have got you covered.
Next Steps
- Read a related article on Phys.org: “Using Fluid Dynamics to Perfect Crêpe Cooking Techniques“
- Read more about fluid-structure interactions on the COMSOL Blog: Modeling Fluid-Structure Interaction in Multibody Mechanisms
MATLAB is a registered trademark of The MathWorks, Inc.





Comments (0)