
In Part 2 of our blog series on how to model irregular shapes in the COMSOL Multiphysics® software, we focus on how to create a surface of an irregular shape based on elevation data stored in various formats such as text, an image, or a DEM file. This approach is best suited for data where the height (or elevation) is a function of x– and y-coordinates.
Example of an Irregular Shape: The Matterhorn Mountain
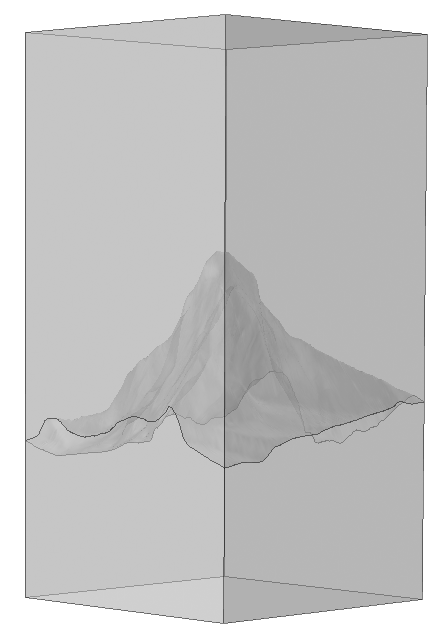
In the previous blog post, we discussed how to loft a geometry from imported curve data using the human head as the example of an irregular shape. Today, let’s discuss the Matterhorn, a European mountain, as an example of an irregular shape. This mountain of the Alps, which borders Switzerland and Italy, has a summit of 4478 meters (or 14,692 feet).

The east and north faces of the Matterhorn. Photo from camptocamp.org. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
Height data is the typical format we have when describing geographical data. Today, we’ll discuss how to import elevation data to model the irregular shape of the Matterhorn’s surface. In short, the procedure includes:
- Importing elevation data from a text file, image file, or DEM file into a function feature
- Creating a parametric surface based on the function defined in the previous step
- Uniting the surface with a solid to obtain the computational domains
- Removing unwanted domains (optional)
Now, let’s take a look at how to create a solid geometry of the Matterhorn in COMSOL Multiphysics.
Creating Interpolation, Image, and Elevation Functions
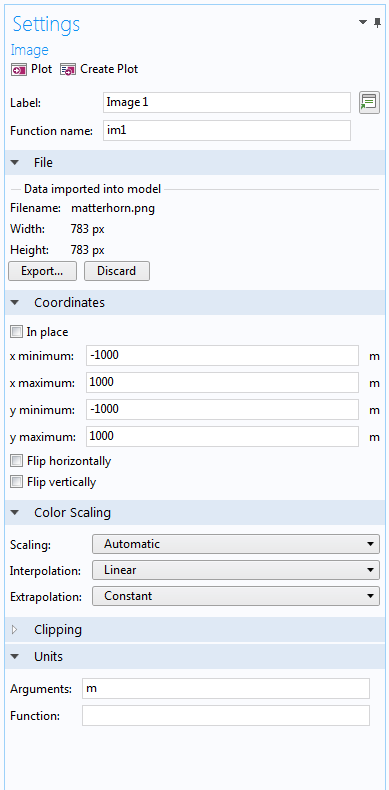
We will use both a text file and grayscale image of the mountain’s height to create a model geometry resembling the Matterhorn. The text file is imported in an Interpolation function, while the picture is imported in an Image function. We’ll also briefly cover importing a DEM file into an Elevation function, but this is not included in the example MPH-file that can be downloaded at the end of this blog post.
In the Image function, we specify the actual maximum and minimum values in the x and y directions, as the picture only contains information on the number of pixels and the color of each pixel. As the dimensions of the geometry are 2000 meters in size, the minimum and maximum values of x and y are set to -1000 m and 1000 m, respectively. Note that if the functions are used in the definitions of the materials or physics, it is also possible to add the units of the arguments and the function.
The Settings windows of the Interpolation function (left) and the Image function (right). The size and position of the region are defined by the text file used in the Interpolation function, while the actual size of the region must be set for the Image function.
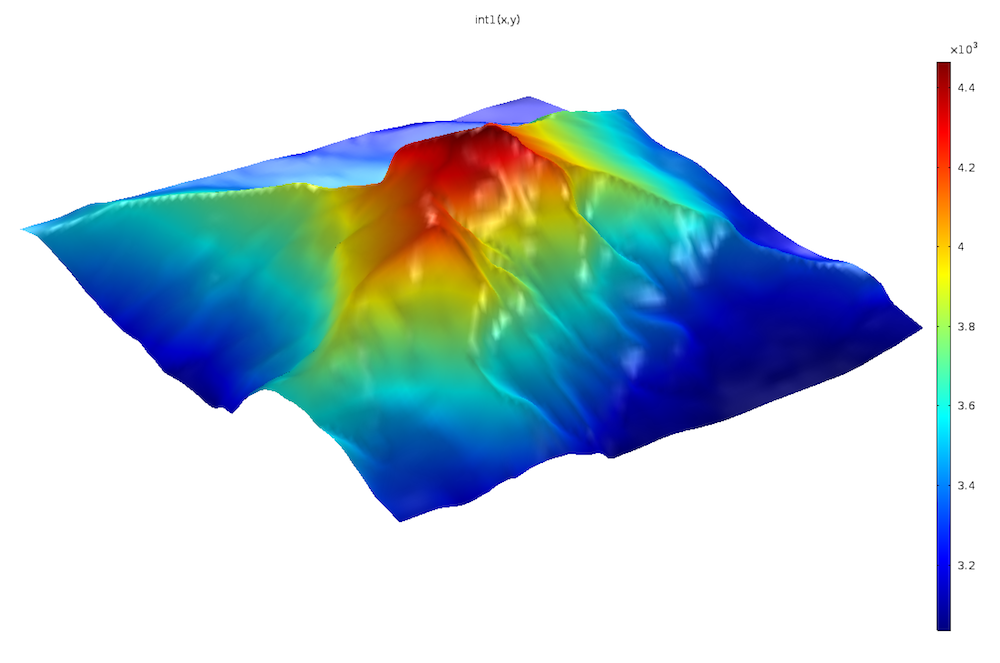
A plot showing the Interpolation function of the imported text file (left). Imported data: DHM25 © swisstopo. The color bar values represent the actual height of the mountain. The grayscale image (right) shows the height of the mountain. Note that the color bar is normalized to go from 0 to 1.
If the geographical data is in a DEM file, it is more suitable to create an Elevation (DEM) function. If the region specified in the DEM file isn’t rectangular, we can specify a height to use outside this region in the Replace missing data with edit field. In the example below, the height of the surface is set to 0 m.
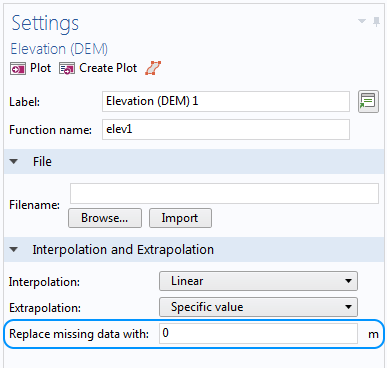
An Elevation (DEM) function is used whenever a DEM file is imported. Enter a value in the Replace missing data with edit field if the region defined in the file doesn’t fill up a rectangular area. The default value is set to 0 m.
Creating Parametric Surfaces
As the underlying data is now available in the model, let’s move on to creating the actual shape of the mountaintop. We use a Parametric Surface feature for this purpose.
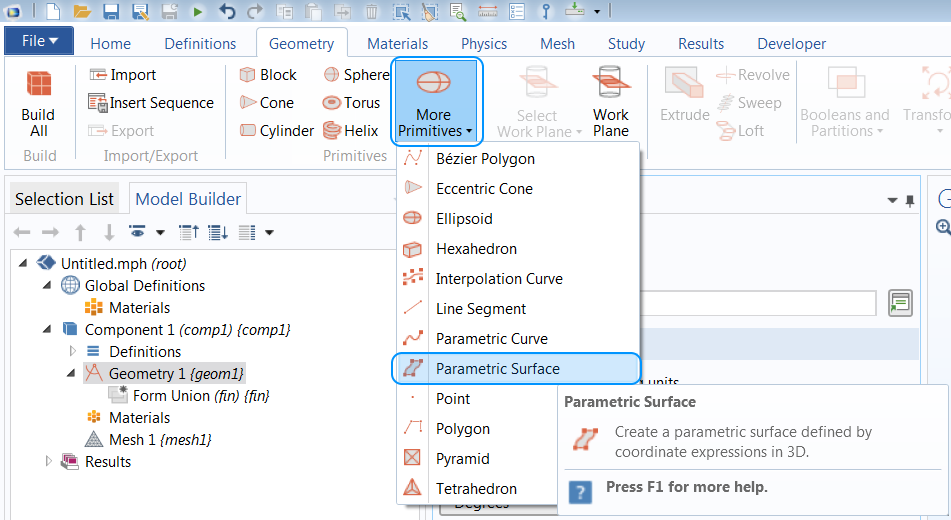
The Parametric Surface feature is found under More Primitives in the Geometry ribbon.
The procedure is quite easy when a DEM file is imported, as we can just click the Create Surface button. This sets up a Parametric Surface feature with the maximum and minimum values in the parameter directions from the DEM file already filled in.
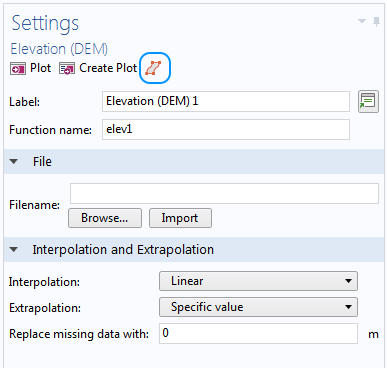
To create a parametric surface based on an imported DEM file, click the Create Surface button.
As the functions are slightly different, the expressions used will also differ. It is recommended to let the two parameters (s1 and s2) go from 0 to 1, so to get the actual dimensions in the final geometry, we need to reparameterize the x-, y-, and z-expressions.
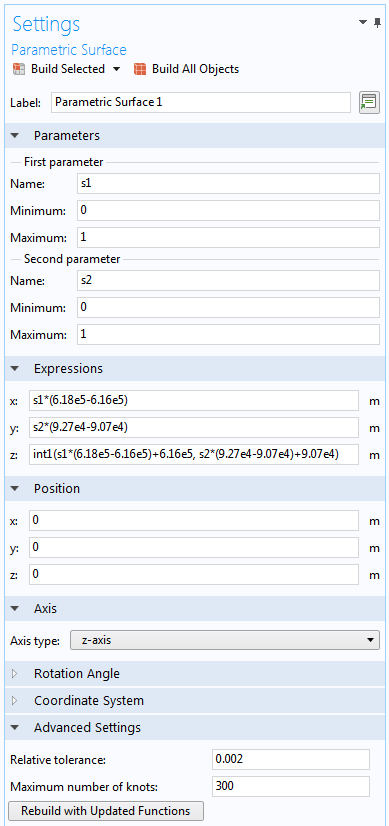
For the Interpolation function, which is defined using the real dimensions of the Matterhorn, the expressions will look like those shown below. One way of obtaining the maximum and minimum values in the x and y direction is to first build the Parametric Surface without rescaling the expressions and then measure the x and y positions of the corners of the created surface. An alternative is to import the coordinate data into a spreadsheet editor, where it is possible to rearrange the coordinates in increasing order.
x: s1*(6.18e5-6.16e5) m
y: s2*(9.27e4-9.07e4) m
z: int1(s1*(6.18e5-6.16e5)+6.16e5, s2*(9.27e4-9.07e4)+9.07e4) m
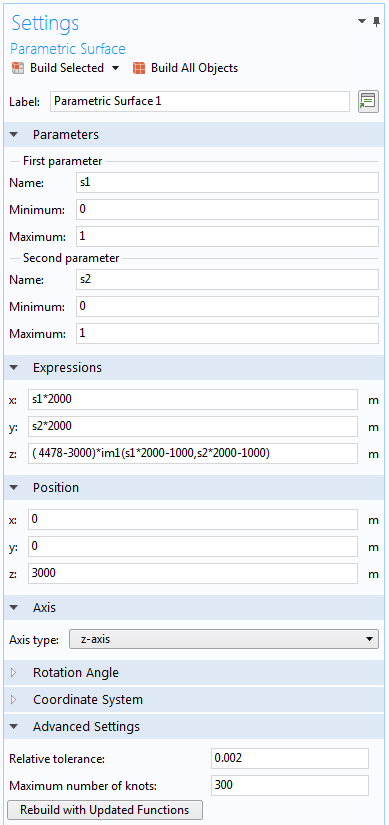
The expressions in the Image function, in which x– and y-values go from -1000 m to 1000 m and output values go from 0 to 1, will instead look like this:
x: s1*2000 m
y: s2*2000 m
z: (4478-3000)*im1(s1*2000-1000,s2*2000-1000) m
Note that we also need to scale the values in the z direction when using an Image function, as it is normalized to go from 0 to 1. In the Settings windows shown below, you can see that the z position changes to 3000 to translate the surface to the correct position in space.
To get a better representation of the surface, the Maximum number of knots is increased to 300 (the default value is 20). This means that the rectangular area will be divided into, at maximum, 300 pieces in both parameter directions, creating patches. The more knots that are allowed, the more flexibility is given to adjust the patches to the given z expression, thereby improving the chances of achieving a tighter relative tolerance.
The algorithm starts by dividing the whole area into a smaller number of patches and then increasing the number of patches where the error is large. By allowing a larger number of knots, the relative error between the patch placements and the actual data points is decreased. The algorithm tries to reach the set Relative tolerance (default value is 1.0E-6) by adding more knots.
When it isn’t possible to reach the tolerance, which can happen if the Maximum number of knots is set too low, a warning will be issued stating which tolerance has been used to build the surface. To remove the warning, copy the tolerance from the Warning node and paste it into the Parametric Surface feature and build it once more.
In the examples used here, the Relative tolerance is manually set to 0.002. If the number of knots is too large, it will result in a heavy geometry operation when creating the surface. There is a balance between using enough knots to get a small relative error and keeping the number of knots low enough so that the operation completes in a reasonable time. Sometimes, a smoother surface is a desired outcome, for instance, if the surface definition contains noise. In that case, reducing the Maximum number of knots will provide a surface that does not follow the noise too closely.
Settings windows of the two Parametric Surface features. The expressions have been reparameterized to keep the two parameters normalized. An increased Maximum number of knots is used to get a better representation of the surfaces.
Creating a Solid
Regardless of which method we have followed, we should now have a geometric surface object that represents the surface of the Matterhorn. However, in most simulations, a solid domain is needed. To do so, we add a Block with a size and location so that the Parametric Surface intersects the block.
The two geometry objects are then added to a Convert to Solid feature. The Convert to Solid operation creates a union of the block and surface, and in addition, it removes any parts of the surface that are sticking out of the block. In this case, where the block perfectly fits the outer edges of the surface, we could also use a Union operation and it will work just as well. Combining the surface and the block results in a solid object that consists of two domains separated by the surface of the Matterhorn.
Resulting geometries after building the Convert to Solid feature. The image to the left shows the irregular surface based on interpolated data from text file and the right-hand image shows the one based on a grayscale image.
The procedure described in this blog post can be used to create a sandwich-type geometry, where the imported surfaces separate different materials, for example, if you want to take a look at the stresses in the layers of rock with different properties. In this case, follow the same procedure to generate each surface and include them all in the Convert to Solid feature.
Forming the Final Geometry
We now have a geometry of the mountain that we can use for meshing and simulation. However, if we are only interested in an analysis of the rock, we can easily remove the upper domain that represents the air. A Delete Entities feature can be used to remove the air domain by setting the Geometric entity level to Domain and adding “domain 2” to the selection. Now, if we rotate the mountain, we can see the resemblance to the photo of the Matterhorn shown at the beginning of the post.
The final geometries created using a text file (left) and an image (right) as input. Imported data: DHM25 © swisstopo.
Concluding Thoughts on Modeling Irregular Shapes Using Different Data Types
Even though the two mountaintop geometries are very much alike, they still differ from each other. If meshed with equal mesh sizes, they will give slightly different meshes. This is in part due to the fact that the Interpolation and Image functions give slightly different inputs to the Parametric Surface feature.
The Parametric Surface feature itself also makes an interpolation when it adapts the surface to the knots described above, so there are two interpolations involved here. However, as long as the size of the mesh is larger than the error of the two mentioned interpolations, it will be an adequate approximation of the imported data.
Further Reading and Next Steps
Irregular shapes can also come in other types of file formats. In a previous blog post, we discuss how to create geometries out of imported meshes. Next in this series, we will demonstrate how to interpolate material data on a regular-shaped domain.
Download the file used to create the example featured here via the button below.









Comments (12)
Mauro Häusler
November 30, 2018Hi there – I am having troubles reproducing the “convert to solid step”: I am not able to select any input objects. I already checked that one: https://www.comsol.com/support/knowledgebase/838/, but was not successful. Actually, I can import ONE object via “past selection” in the “convert to solid” settings, and typing in the object name, but I cannot add the second. Do you have any idea, what can go wrong? Thanks a lot – and sorry if the question is trivial – I just started with COMSOL.
Hanna Gothäll
November 30, 2018Hi Mauro – Thank you for your interest in this blog post! It is unclear from your description what may be happening here. Please send in your model MPH file along with a description to COMSOL Support ( support@comsol.com or https://www.comsol.com/support/case/ ) so that we can have a look at the file.
Hassan Liaquat
December 24, 2021Hi There, please tell me What do you mean by Text file? how to get that file
Hanna Gothäll
January 11, 2022 COMSOL EmployeeDear Hassan,
In this context, a “text file” refers to a file with extension TXT on either of the data formats grid, sectionwise, or spreadsheet. Read more about these data formats in the COMSOL Multiphysics Reference Guide. These type of files can be either exported from COMSOL Multiphysics, be scanned data (as in the case of the Matterhorn data used in the blog post), be data exported from another software, …
Claire Puleio
April 5, 2022Hi there-
I am using COMSOL 6.0 – how do I create a parametric surface when using an imported DEM? I do not see a Create Surface button next to Create Plot under Elevation (DEM).
Thank you!
Hanna Gothäll
April 6, 2022 COMSOL EmployeeHi Claire,
You need to manually select Parametric Surface from the More Primitives menu on the Geometry tab, or from the Model Builder context menu. Then, set up the Parametric Surface in the same way as described for the Interpolation and Image functions in the blog post. If you don’t know the maximum and minimum values of your Elevation (DEM) function, I recommend to click the plot button in the Settings window for the function and derive the values from the plot.
Claire Puleio
April 6, 2022Thank you Hanna for your quick reply!
Eric Grosfils
November 18, 2023Hi — this was a fun and useful post! Thanks. General question. Having defined the topographic parametric surface, is there a way to automatically obtain the z value of that surface for any generic (x,y) location one might select? As I vary (x,y) I’d like to identify the corresponding elevation value to use elsewhere in the model. Thanks!
Hanna Gothäll
November 20, 2023 COMSOL EmployeeHi Eric,
I’m glad to hear that the blog post was useful. I suggest that you use your Interpolation/Image/Elevation function for that purpose: int1(x,y)/im1(x,y)/elev1(x,y). It might not be the exact value as if you would measure on the parametric curve, but it is the closest you have. If you need further help, send your MPH file to support@comsol.com.
Eric Grosfils
November 21, 2023Thanks Hanna — that appears to have done the trick. It should work well for my purposes. I had been focused on the ps1 product, hadn’t occurred to me to try its source. Much appreciated!
Dima BH
February 5, 2024Hello,
I am trying to do the same my model is 2D I’ve started with interpolation of txt file and create
the surface profile, but now I want to use a parametric curve ( my model is 2D) what the expression should be used to fit my geometry my geometry is a ring with 2.5mm radius and thickness of 25um I want the outer curve of the surface has different topology based on my surface profile
thank you
Hanna Gothäll
February 6, 2024 COMSOL EmployeeDear Dima,
If you intend to create a 2D geometry, I would instead recommend that you set up a Grid 2D dataset for int1(x,y), and then use a Filter or Partition dataset similar to what is done in the first part of this blog post:
https://www.comsol.com/blogs/generating-a-simulation-mesh-of-a-femur-from-3d-data/
As you work in 2D, you need to use Remesh Domains (new for v6.2) to improve the mesh in the domain(s).
If you need further assistance, please send your txt file and mph file to support@comsol.com so that we can give more detailed advice.